This algorithm comes in three parts: defining the Game Environment, the Monte-Carlo Search Tree (MCTS) methods and a Neural Network that deduces the action to choose from a given state of the board.

1. Game Environment

The first step in reinforcement learning is to define the environment our agent will be trained on. This means defining what are the possible states, actions and associated rewards. Here we will consider any two players zero sum board game with complete information such as Tic-Tac-Toe, Othello or Go. Let us first define the game states and actions.

Game State and Actions

The game state is a given configuration of the board: it can be represented by a matrix where each cell is described by the color of the token placed. The list of possible actions is game-specific: for Go it will be all empty cells but there will be less possible actions in Othello.

Rewards

In order to learn, the agent must be given rewards. But these rewards can’t be known at each step. At first, the only information available is the reward at game end: the player gets a reward of +1 for winning, 0 for draw and -1 for losing. Unfortunately, a game can end after hundreds of moves in extremely diverse configurations. An agent can’t compute all possible paths leading to a victory. The idea is to infer value associated to various positions by playing hundred of thousands of games. Therefore, our agent must search the environment through self-play.

2. Self Play

The agent performs self play by performing Monte Carlo Search according to a search probability U.

Monte Carlo Tree Search

The idea of Monte Carlo Search is to perform several rollouts to better estimate the value of the configuration visited. The agents stores the configuration it has visited in a Tree.

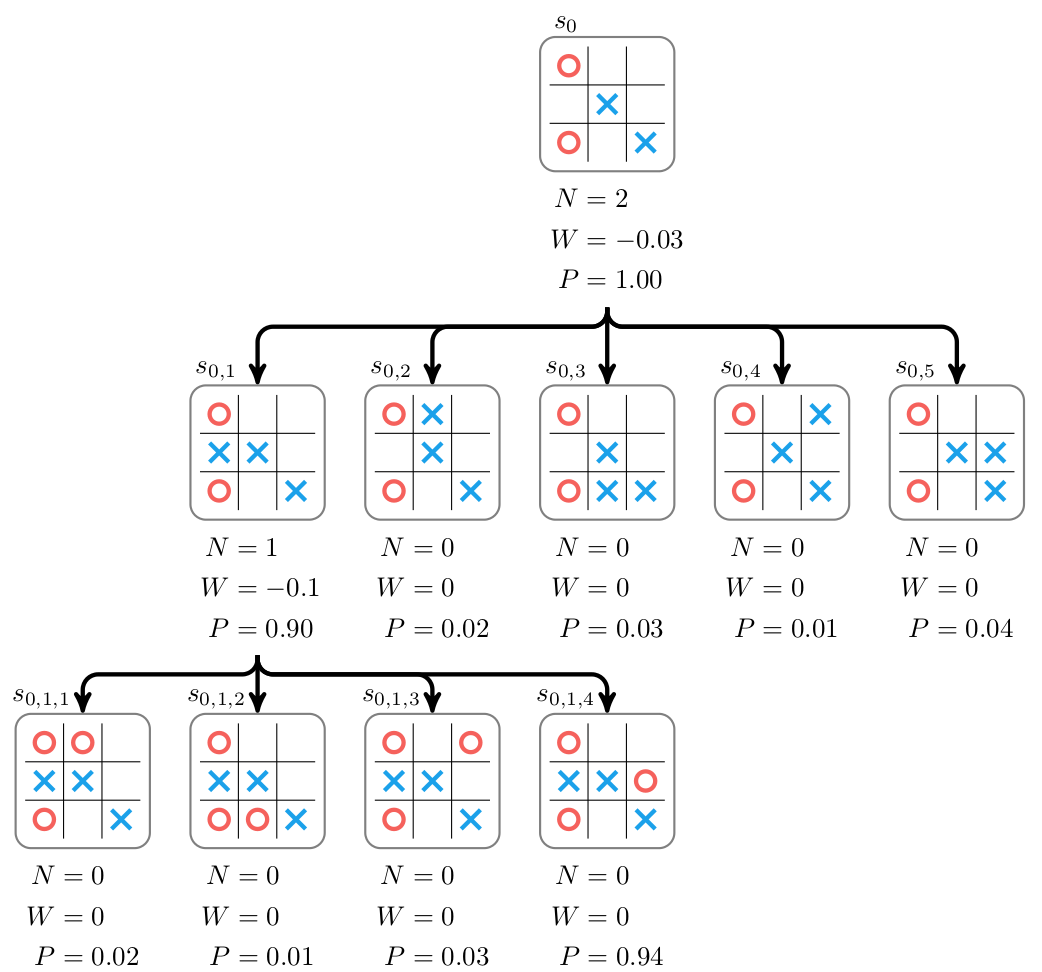
The Tree Search is performed according to a specific rule: the Search Probability U.

Search probabilities

The search probabilities rely upon a neural network that infer a position value from previously obtained data. The new data obtained during the search will be fed into a new network to obtain a more accurate estimation of position value. Therefore this algorithm goes back-and-forth between creating data from a previous network and training a new network on these new data.
The deep network part is developed in the Learning section.

Let us consider a state S and perform a simulation : we choose the action A that maximizes a utility function U(S, A) defined by : $$ U(S, A) = Q(S, A) + c_{puct} . P(S, A) . \displaystyle{\frac{\sqrt{\sum_b N(S, b)}}{1 + N(S, A)}} $$ where

• N(S, A) is the visit counter : action A has been taken N(S, A) times from node S
• Q(S, A) is the expected reward from playing action A at node S
• P(S, A) is the initial policy given by the neural network
• c_puct is a hyperparameter tuning the degree of exploration.

After playing action A , we update visit counter N(S, A) and we get to the new node S’ .
S’ is either newly visited, in which case we simply add this node to the tree, and initialize N(s’, b) and Q(s’, b) to 0 for all actions b while calling the neural network for the policy P(s’, .).
In the other case, it has already been visited and then we call the function rollout recursively on s’ until a new node or a terminal state is reached. In that case we back propagate to update all expected rewards Q(s, a) in the path.

Update policy

Once all rollouts have been performed and all values updated, we have produced examples. Theses will be turned into values Q(s, .) by taking the empirical mean of the visit counter N(s, .) and normalizing it. During a real game against a player, the agent will choose at state s the action a^* = argmax_a(Q(s, a)).

3. Learning

The objective of our algorithm is to find the optimal move for any given state of the board. It would be impossible to store all configurations of the board and perform tabular Q-learning. Therefore we need an algorithm that can deduce from one given input its value. The network implemented for Alpha Zero is a Convolutionnal Neural Net that takes a 2D grid as input and outputs a value for this state. In order for any machine learning algorithm to discover what makes a good state and, consequently, a good action it requires lots of data, i.e game configurations labelled with its associated value.

Training Data

As we said, we don't have ground truth value for any configuration of the board except when the game as ended. The only information available are estimates of state-action values Q(., .) computed during the rollouts. Therefore the network learns from data obtained by a previous iteration of the same network. It estimates a position based on data acquired from its previous estimates. Therefore we say that the network is bootstraping the values of the board game.

Evaluating network

Once the new network has been trained on the new data, we can compare its performance against the previous network by making them play together. The new network has to win 55% of the showdowns to be considered as the new best network. It will then be used for the next step of the learning iteration.
We will coninue this process until we have reached a convergence where the new network never show progress conpare to the previous one.